Uno: Why am I drawing so many cards?

Introduction

I was playing Uno with a friend, and he had just played a red '1' card. I didn't have a red, a '1' or a wild card in my hand. Nothing in my hand matched a red '1', so I had to start drawing cards.

I drew one card and it did not match. I drew another and missed again. And another. And so on... In the end, I drew eight cards until I got a match. This seemed like a lot to me, but I didn't think too much about it and we continued to play.

To my surprise, I found that several more times during that game I drew seven or more cards until I got one that matched!

An Uno deck has only four colors - what was the probability of drawing seven cards or more to find one that matched on color, nevermind cards that match the number - or wild cards?

TLDR: the probability of drawing seven or more cards until the first match is 8.89%, to three significant figures (s.f.). Read on to learn about the caveats...

Exploring the problem

I wanted to understand the problem better. One fun way to explore a problem is to write a simulation of it.

However, I decided to keep the simulation simple and focused on the common case so I could get to the heart of the matter without getting bogged down in tangential complexities. I did not want to simulate an entire game of Uno. So my simulation would perform three steps:

Draw a card from a full, shuffled Uno deck. This card would be the 'top card' in the discard pile.
If the top card drawn in Step 1 is numbered 1-9, then proceed to Step 3. Otherwise, ignore it and start over at step 1.
Now draw another card from the deck and see if it matches the top card drawn in step 1. If not, draw more cards until a match is found. Return the total number of cards drawn to achieve a match.

I wrote my simulation of these steps in Ruby and the code is here.

I then ran 10 simulations using a rake task (Ruby's version of make) and the results are below.

$ rake run[10]
4 1 2 2 2 1 1 1 5 4

So, in the first simulation, four cards were drawn until a match was found. In the second simulation, only one card was drawn to get a match, and so on.

So far, so good. I then ran my simulation 100,000 times. The table below shows the frequency counts for getting a match after drawing one card, two cards, etc. up to 10 cards.

\begin{array}{cc} \hline \text{number of cards drawn} & \text{frequency} \\ \hline 1 & 32{,}437 \\ 2 & 22{,}039 \\ 3 & 14{,}826 \\ 4 & 10{,}279 \\ 5 & 6{,}877 \\ 6 & 4{,}615 \\ 7 & 2{,}959 \\ 8 & 2{,}109 \\ 9 & 1{,}369 \\ 10 & 859 \\\hline \end{array}

Below is a bar chart of the same data. The code for generating the bar chart and doing the rest of the math in this post can be found in this Julia notebook.

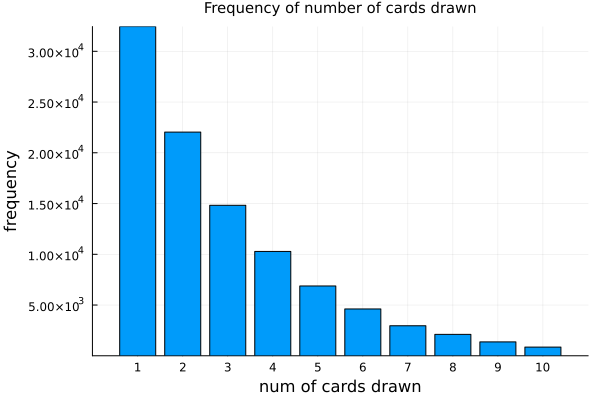
histogram

The table shows that in 32,437 cases, the first card drawn matched the top card. In 22,039 cases, it took two draws from the Uno deck to find a matching card, and so on.

After squinting at the discrete, right skew bar chart a bit, I realized it reminded me of a Geometric distribution. This makes some sense. Each card drawn from the deck can be thought of as a Bernoulli trial. When the card matches the top card, the trial is a success - otherwise, it is a failure.

Since a Geometric distribution models the number of Bernoulli trials required to obtain the first success, this almost fits my scenario.

….However, there is a problem. An assumption of the Geometric distribution is that the probability of success of each trial is the same across all trials. But that's not true for Uno.

In Uno, if a card is drawn and it does not match, on the next draw the deck has the same number of matching cards, but one fewer non-matching card. So the probability of drawing a matching card improves a little bit between trials. Hence the assumption of a constant probability of success between trials does not hold.

The right distribution

So, if the Geometric distribution was not an exact fit for this scenario, I wanted to find one that was. I searched the internet a bit and I found this paper^[1] by John Ahlgren (2014) which describes this situation exactly.

Instead of cards, Ahlgren describes a scenario in which there are N objects in an urn, of which K are 'good'. The question is then how many draws from the urn are necessary to get the first good object.

Ahlgren characterizes the distribution with formulas for the mean, the probability mass function (pmf) and the cumulative distribution function (cdf), among other things. I've implemented those formulas here and written some tests for that code here.

The mean of the distribution is given by

\begin{aligned} E(X) & =\frac{N + 1}{K + 1}\\ \end{aligned}.

An Uno deck has 112 cards. After drawing the top card, there are $N=111$ cards left, of which $K=36$ will match. Please see the fine print below for an explanation of how I arrived at the number 36. Applying the formula for the mean with these parameters we have:

\begin{aligned} E(X) & =\frac{36 + 1}{111 + 1} \\ & = \frac{37}{112} \\ & \approx 3.03. \qquad \text{(to 3 s.f.)} \\ \end{aligned}

So if an Uno player is forced to draw cards from the deck on their turn, they can expect to draw about 3 cards in total.

Turning to the pmf, Ahlgren supplies the following formula:

\begin{aligned} P(X = x) & =\frac{N-x+1 \choose K}{N \choose K} \times \frac{K}{N-x+1}\\ \end{aligned}

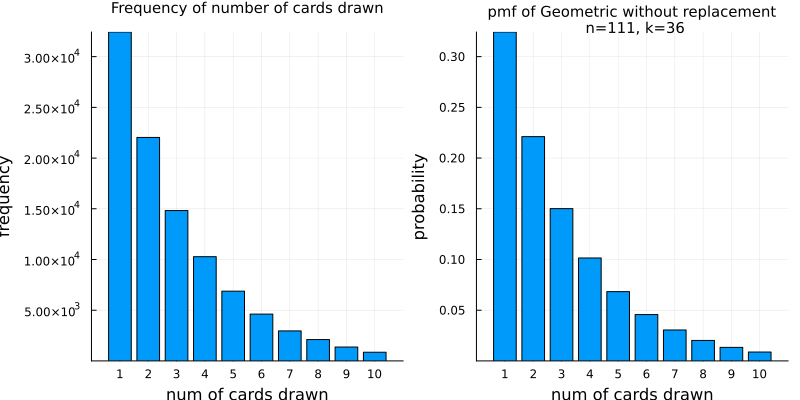
Calculating specific values for X in my scenario where $N=111$ and $K=36$ , we have:

\begin{array}{cc} \hline \text{x = number of cards drawn} & \text{P(X = x)} \\ \hline 1 & 0.324 \\ 2 & 0.221 \\ 3 & 0.150 \\ 4 & 0.101 \\ 5 & 0.068 \\ 6 & 0.046 \\ 7 & 0.030 \\ 8 & 0.020 \\ 9 & 0.013 \\ 10 & 0.009 \\ \hline \end{array}

So, from the table, the probability of getting a matching card on the first draw is 0.324, which is simply 36/111 to three decimal places, which makes sense. The probability of getting the first match on the second draw is 0.219, and so on.

Eyeballing plots of this pmf alongside frequency counts from my simulation above gave me some reassurance that I was on the right track. A better approach would be to code up a QQ plot, but I ran out of time.

sidebyside

Back to the question

So how often should I draw seven cards or more? Ahlgren's formula for the cdf is:

\begin{aligned} P(X <= x) = F(x) & =1-\frac{N-x \choose K}{N \choose K} \\ \end{aligned}.

So the probability that we'll have to draw seven cards or more is:

\begin{aligned} P(X >= 7) = 1 - P(X <= 6) & = 1 - F(6)\\ & = \frac{111 - 6 \choose 36}{111 \choose 36}\\ & \approx 0.0889 \qquad \text{(to 3 s.f.)} \\ \end{aligned}

So, we can expect to draw seven cards or more about 8.89% of the time. It's fairly rare.

So why was I drawing so many cards?

Well, one key assumption in the scenario is that the Uno deck is well shuffled.

However, the process of playing Uno naturally sorts the cards into runs of the same color or number. So it is very important that the cards are well shuffled between games. Were we shuffling the cards enough? I would guess that we were shuffling the deck about five times between games.

Was that enough? Well, there is some interesting work published on card shuffling. In particular, Bayer and Diaconis (1992) showed that about $\frac{3}{2}\log_{2}(n)$ shuffles are required to properly mix up n cards^[2]. For an Uno deck of 112, cards, this is approximately 10.21 shuffles. So we were not shuffling enough!

Conclusions

In retrospect, this seems like the obvious answer. However, you might have an opponent who will claim that the reason you're drawing so many cards is down to their skill at Uno. That may be true in part, but I would keep still shuffle the card thoroughly between games to be sure 😉.

The fine print

I made some design choices in my study to focus on the common case. I'll try to justify those choices here.

1. My buddy and I play with this version of Uno. In this deck, there is one card numbered '0' for each color: red, green, blue and yellow. However, there are two cards numbered 1-9 for each color. I think the game designers only included one '0' card per color because these are very useful if you are keeping score between games.

action cards

In any event, if the top card on the discard pile is a '0', the odds of drawing a matching card from the deck are slightly lower than any other numbered card, simply because there are only three other '0's in the deck. However, if the top card is a '1' (or any other numbered card), there are seven other '1' cards in the deck and your chances of drawing a match are therefore better. So, I chose to ignore the case where a '0' is the top card.

action cards

2. In two-player Uno, if you play a 'skip', 'reverse' or 'draw 2' card, your opponent forfeits their turn and you start another turn. "Skip you" says my buddy when he plays one of these cards... If you don't have another card matching that color, you will have to start drawing more cards from the deck.

So if you draw one of these cards, you can play it, but you're not really off the hook. You will have to keep drawing more cards. Hence, if one of these cards is drawn, I do not consider them to be a match. There are further caveats on this, but this is far enough down the rabbit hole I think.

3. The Uno deck has 112 cards. 12 of those are wild and the remaining 100 are colored, 25 of each color.

A breakdown of the colored cards is shown in the table below.

\begin{array}{cc} \hline \text{card type} & \text{number of cards per color} \\ \hline \text{'0's} & 1 \\ \text{'1'-'9's} & 2 \times 8 = 16 \\ \text{skip} & 2 \\ \text{reverse} & 2 \\ \text{draw 2} & 2 \\ \hline \text{total} & 25 \\ \hline \end{array}

Now, given notes #1 and #2 above, if a 'red 1' card is the top card on the discard pile, there are 36 other cards that 'match' that card. Here is a breakdown of the cards matching that 'red 1'.

\begin{array}{cc} \hline \text{card type} & \text{number of cards} \\ \hline \text{red '0'} & 1 \\ \text{red '1'} & 1 \\ \text{red '2'-'9'} & 2 \times 8 = 16 \\ \text{blue, green and yellow '1's} & 6 \\ \text{wild} & 12 \\ \hline \text{total} & 36 \\ \hline \end{array}

Hence there are 36 cards in a full deck that match a 'red 1'.

References

[1]	Ahlgren, J. (2014, April 4). The Probability Distribution for Draws Until First Success Without Replacement. ArXiv.org. https://doi.org/10.48550/arXiv.1404.1161

[2]	Bayer, D. and Diaconis, P. (1992) Trailing the Dovetail Shuffle to Its Lair. The Annals of Applied Probability, 2 294-313. https://doi.org/10.1214/aoap/1177005705

CC BY-SA 4.0 Joshua Whittemore. Last modified: February 09, 2024. Website built with Franklin.jl and the Julia programming language.